A remark about the embedding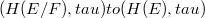 
, with 
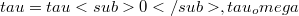, in Frechet spaces
Abstract
In a recentpaper by Aron-Moraes-Ryan [2], it is proved that when E is a complex Banach space, F is a closed subspace of E and U is a balanced open subset of E, then the mapping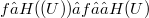 
where 𝜋 is the canonical mapping from E onto 
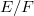, is a topological isomorphism from 
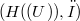onto a closed subspace of 
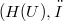, where 
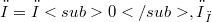. The aim of this remark is to show that the same result is true, with 
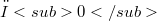for Fréchet spaces, and with 
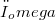for Fréchet-Schwartz spaces. Also we prove that this result is not true, with 
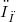for some Fréchet-Montel spaces and with 
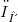for some nuclear Fréchet spaces.
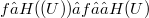where 𝜋 is the canonical mapping from E onto 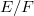, is a topological isomorphism from 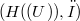onto a closed subspace of 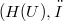, where 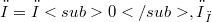. The aim of this remark is to show that the same result is true, with 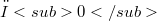for Fréchet spaces, and with 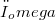for Fréchet-Schwartz spaces. Also we prove that this result is not true, with 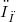for some Fréchet-Montel spaces and with 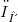for some nuclear Fréchet spaces.DOI Code:
10.1285/i15900932v9n2p217
Full Text: PDF
