Functional differential inequalities of parabolic type
Abstract
We prove a theorem wich generalizes a result of J. Szarski (see [4];Theor. 2)concerning weak inequalities fora diagonal system of second order differential functional inequalities of hetype(Error rendering LaTeX formula) 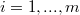 , assuming that
, assuming that 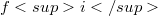 is parabolic with respect to u for any
is parabolic with respect to u for any 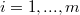 . After introducing the definition of left parabolic (or right parabolic) function with respect to another one, we obtain the over mentioned generalization (Theor. 2.2) as a consequence of a theorem about strong inequalities (Theor. 2.1) which is a generalization of Theor.1 of [4] in the case of left parabolic (or right parabolic) functions. These generalizations have been suggested by the following example in wich we have the assertion of Theor. 2 of [4] even if hypotheses of the theorem are not al1 verified. Consider the function f defined as (l)(Error rendering LaTeX formula) for(Error rendering LaTeX formula) belonging to the set of real and symmetried 2 x 2 matrices and z continuous function in Đ, with continuous in D partial second derivatives with respect to x as well as functions u and v defined assuming
. After introducing the definition of left parabolic (or right parabolic) function with respect to another one, we obtain the over mentioned generalization (Theor. 2.2) as a consequence of a theorem about strong inequalities (Theor. 2.1) which is a generalization of Theor.1 of [4] in the case of left parabolic (or right parabolic) functions. These generalizations have been suggested by the following example in wich we have the assertion of Theor. 2 of [4] even if hypotheses of the theorem are not al1 verified. Consider the function f defined as (l)(Error rendering LaTeX formula) for(Error rendering LaTeX formula) belonging to the set of real and symmetried 2 x 2 matrices and z continuous function in Đ, with continuous in D partial second derivatives with respect to x as well as functions u and v defined assuming 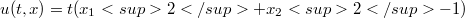 and
and 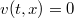 for every
for every 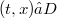 .
.
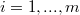 , assuming that
, assuming that 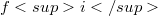 is parabolic with respect to u for any
is parabolic with respect to u for any 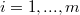 . After introducing the definition of left parabolic (or right parabolic) function with respect to another one, we obtain the over mentioned generalization (Theor. 2.2) as a consequence of a theorem about strong inequalities (Theor. 2.1) which is a generalization of Theor.1 of [4] in the case of left parabolic (or right parabolic) functions. These generalizations have been suggested by the following example in wich we have the assertion of Theor. 2 of [4] even if hypotheses of the theorem are not al1 verified. Consider the function f defined as (l)(Error rendering LaTeX formula) for(Error rendering LaTeX formula) belonging to the set of real and symmetried 2 x 2 matrices and z continuous function in Đ, with continuous in D partial second derivatives with respect to x as well as functions u and v defined assuming
. After introducing the definition of left parabolic (or right parabolic) function with respect to another one, we obtain the over mentioned generalization (Theor. 2.2) as a consequence of a theorem about strong inequalities (Theor. 2.1) which is a generalization of Theor.1 of [4] in the case of left parabolic (or right parabolic) functions. These generalizations have been suggested by the following example in wich we have the assertion of Theor. 2 of [4] even if hypotheses of the theorem are not al1 verified. Consider the function f defined as (l)(Error rendering LaTeX formula) for(Error rendering LaTeX formula) belonging to the set of real and symmetried 2 x 2 matrices and z continuous function in Đ, with continuous in D partial second derivatives with respect to x as well as functions u and v defined assuming 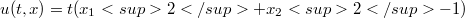 and
and 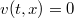 for every
for every 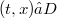 .
.DOI Code:
10.1285/i15900932v9n2p173
Full Text: PDF


