A structure theorem for echelon Köthe spaces
Abstract
In [9], Lopez-Molina defined the echelon Köthe spaces 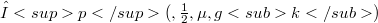 , which provide a suitable generalization of the echelon sequence spaces
, which provide a suitable generalization of the echelon sequence spaces 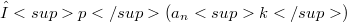 to a general measure space
to a general measure space 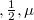 (see also [5]). In this paper, we show that the strutture of the separable echelon Köthe spaces is «nicely» close to the strutture of the echelon sequence spaces. Namely, our main result is: Let
(see also [5]). In this paper, we show that the strutture of the separable echelon Köthe spaces is «nicely» close to the strutture of the echelon sequence spaces. Namely, our main result is: Let 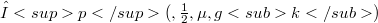 be a separable echelon Köthe space of order p,
be a separable echelon Köthe space of order p, 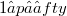 , with
, with 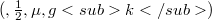 purely non-atomic. Then, there is an echelon sequence space
purely non-atomic. Then, there is an echelon sequence space 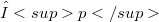 so that
so that 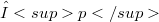 is isomorphic to the space
is isomorphic to the space 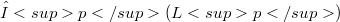 of all
of all 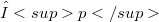 -summable sequences in
-summable sequences in 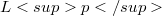 . An an application we show that a separable echelon Köthe space has a basis (by a basis we mean a Schauder basis), which is unconditional if
. An an application we show that a separable echelon Köthe space has a basis (by a basis we mean a Schauder basis), which is unconditional if 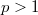 .
.
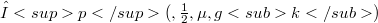 , which provide a suitable generalization of the echelon sequence spaces
, which provide a suitable generalization of the echelon sequence spaces 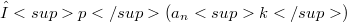 to a general measure space
to a general measure space 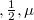 (see also [5]). In this paper, we show that the strutture of the separable echelon Köthe spaces is «nicely» close to the strutture of the echelon sequence spaces. Namely, our main result is: Let
(see also [5]). In this paper, we show that the strutture of the separable echelon Köthe spaces is «nicely» close to the strutture of the echelon sequence spaces. Namely, our main result is: Let 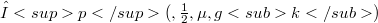 be a separable echelon Köthe space of order p,
be a separable echelon Köthe space of order p, 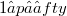 , with
, with 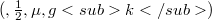 purely non-atomic. Then, there is an echelon sequence space
purely non-atomic. Then, there is an echelon sequence space 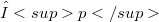 so that
so that 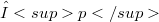 is isomorphic to the space
is isomorphic to the space 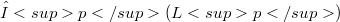 of all
of all 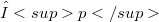 -summable sequences in
-summable sequences in 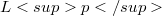 . An an application we show that a separable echelon Köthe space has a basis (by a basis we mean a Schauder basis), which is unconditional if
. An an application we show that a separable echelon Köthe space has a basis (by a basis we mean a Schauder basis), which is unconditional if 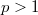 .
.DOI Code:
10.1285/i15900932v9n2p165
Full Text: PDF


