Codimension two product submanifolds with non-negative curvature
Abstract
We prove that if(Error rendering LaTeX formula) is an isometric immersion of a complete, non-compact Riemannian manifold M which is a product of non-negatively curved manifolds 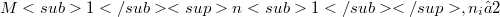 ,
, 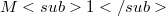 non-flat and irreducible, then either f is
non-flat and irreducible, then either f is 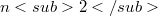 -cylindrical; or f is a product of hypersurface immersions with
-cylindrical; or f is a product of hypersurface immersions with 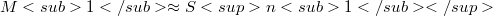 or
or 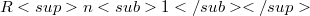 ; or f is
; or f is 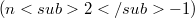 -cylindrical with
-cylindrical with 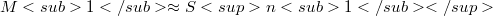 or
or 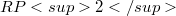 when
when 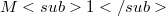 is compact, and
is compact, and 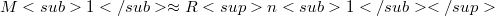 when
when 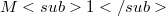 is non-compact.
is non-compact.
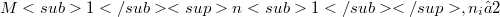 ,
, 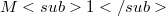 non-flat and irreducible, then either f is
non-flat and irreducible, then either f is 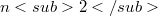 -cylindrical; or f is a product of hypersurface immersions with
-cylindrical; or f is a product of hypersurface immersions with 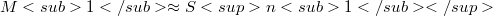 or
or 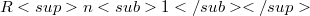 ; or f is
; or f is 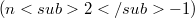 -cylindrical with
-cylindrical with 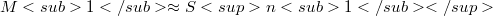 or
or 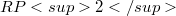 when
when 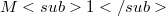 is compact, and
is compact, and 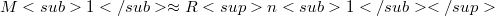 when
when 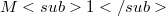 is non-compact.
is non-compact.DOI Code:
10.1285/i15900932v9n1p89
Full Text: PDF


