Smooth points of the positive part of the unit ball of 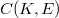
Abstract
Let K be a compact Hausdortf space and let E be a Banach lattice. By 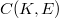 we denote the Banach lattice of E-valued continuous functions on K. The aim of the paper is to characterize explicitly the smooth points and quasi interior points of the positive part of the unit hall of
we denote the Banach lattice of E-valued continuous functions on K. The aim of the paper is to characterize explicitly the smooth points and quasi interior points of the positive part of the unit hall of 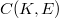 . Then we translate this result to the space of compact operators
. Then we translate this result to the space of compact operators 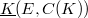 . We describe also extreme points of the positive part of
. We describe also extreme points of the positive part of 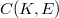 . The description of smooth points as well as extreme and exposed points gives us additional knowledge about the geometry of an important class of convex sets in functional analysis. In this paper we would like to use this tool for the study of the geometry of the positive part of the unit hall of various well-known Banach spaces. In Section 1 we collect general facts about supporting points, smooth points and quasi interior points of the positive part of the unit hall of an arbitrary Banach lattice. Singer [6] has described the extreme points of the unit hall of the space dual to the space
. The description of smooth points as well as extreme and exposed points gives us additional knowledge about the geometry of an important class of convex sets in functional analysis. In this paper we would like to use this tool for the study of the geometry of the positive part of the unit hall of various well-known Banach spaces. In Section 1 we collect general facts about supporting points, smooth points and quasi interior points of the positive part of the unit hall of an arbitrary Banach lattice. Singer [6] has described the extreme points of the unit hall of the space dual to the space 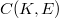 of continuous functions from a compact set K into a Banach space E. In Section 2 we adapt his proof to get an analogous characterization of the extreme points of the positive part of the unit hall of the
of continuous functions from a compact set K into a Banach space E. In Section 2 we adapt his proof to get an analogous characterization of the extreme points of the positive part of the unit hall of the 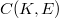 , where E is a Banach lattice. Sundaresan [8] has described smooth points of the unit hall of
, where E is a Banach lattice. Sundaresan [8] has described smooth points of the unit hall of 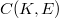 . In Section 3 we continue this for the positive part of the unit hall of
. In Section 3 we continue this for the positive part of the unit hall of 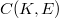 . Moreover we give a characterization of quasi interior points in
. Moreover we give a characterization of quasi interior points in 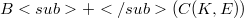 . Then, in Section 4 we apply these results to the space of compact operators
. Then, in Section 4 we apply these results to the space of compact operators 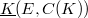 .
.
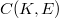 we denote the Banach lattice of E-valued continuous functions on K. The aim of the paper is to characterize explicitly the smooth points and quasi interior points of the positive part of the unit hall of
we denote the Banach lattice of E-valued continuous functions on K. The aim of the paper is to characterize explicitly the smooth points and quasi interior points of the positive part of the unit hall of 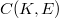 . Then we translate this result to the space of compact operators
. Then we translate this result to the space of compact operators 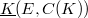 . We describe also extreme points of the positive part of
. We describe also extreme points of the positive part of 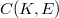 . The description of smooth points as well as extreme and exposed points gives us additional knowledge about the geometry of an important class of convex sets in functional analysis. In this paper we would like to use this tool for the study of the geometry of the positive part of the unit hall of various well-known Banach spaces. In Section 1 we collect general facts about supporting points, smooth points and quasi interior points of the positive part of the unit hall of an arbitrary Banach lattice. Singer [6] has described the extreme points of the unit hall of the space dual to the space
. The description of smooth points as well as extreme and exposed points gives us additional knowledge about the geometry of an important class of convex sets in functional analysis. In this paper we would like to use this tool for the study of the geometry of the positive part of the unit hall of various well-known Banach spaces. In Section 1 we collect general facts about supporting points, smooth points and quasi interior points of the positive part of the unit hall of an arbitrary Banach lattice. Singer [6] has described the extreme points of the unit hall of the space dual to the space 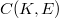 of continuous functions from a compact set K into a Banach space E. In Section 2 we adapt his proof to get an analogous characterization of the extreme points of the positive part of the unit hall of the
of continuous functions from a compact set K into a Banach space E. In Section 2 we adapt his proof to get an analogous characterization of the extreme points of the positive part of the unit hall of the 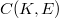 , where E is a Banach lattice. Sundaresan [8] has described smooth points of the unit hall of
, where E is a Banach lattice. Sundaresan [8] has described smooth points of the unit hall of 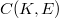 . In Section 3 we continue this for the positive part of the unit hall of
. In Section 3 we continue this for the positive part of the unit hall of 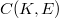 . Moreover we give a characterization of quasi interior points in
. Moreover we give a characterization of quasi interior points in 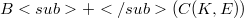 . Then, in Section 4 we apply these results to the space of compact operators
. Then, in Section 4 we apply these results to the space of compact operators 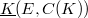 .
.DOI Code:
10.1285/i15900932v10supn2p273
Keywords:
Smooth point; Positive part of unit ball; Quasi-interior point; Vector-valued function; Compact operat
Classification:
46E20; 46B30; 58C20; 46B20
Full Text: PDF


