Generalized sampling approximation of multivariate signals; theory and some applications
Abstract
For a continuous and bounded kernel function 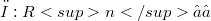 , and a continuous function f the multivariate sampling series is defined by (1.1) (Error rendering LaTeX formula) In [6] the authors presented some qualitative and quantitative theorems on the approximation of
, and a continuous function f the multivariate sampling series is defined by (1.1) (Error rendering LaTeX formula) In [6] the authors presented some qualitative and quantitative theorems on the approximation of 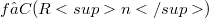 by
by 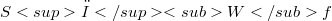 , as well as a few first applications. Some theorems in this respect to be needed below are assertion (5.2) as well as Theorem 5.1 of Section 5. In the more theoretical part of this paper two further quantitative theorems are given. The first deals with the case of product kernels, namely Theorem 3.1, where univariate theory is used to yield convergence theorems with rates in an iterative way, together with an application. The second theorem, Theorem 4.1, is concerned with bandlimited kernels, in which case the convergence with rates of
, as well as a few first applications. Some theorems in this respect to be needed below are assertion (5.2) as well as Theorem 5.1 of Section 5. In the more theoretical part of this paper two further quantitative theorems are given. The first deals with the case of product kernels, namely Theorem 3.1, where univariate theory is used to yield convergence theorems with rates in an iterative way, together with an application. The second theorem, Theorem 4.1, is concerned with bandlimited kernels, in which case the convergence with rates of 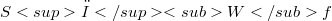 is compared with and deduced from the approximation behaviour of the associated singular convolution integral of Fejér’s type. The matter is applied to three concrete kernels.
The core of this paper is Section 5, devoted to the applications of the general theorems of [6] to box splines, especially to linear combinations of translates of box splines. Basic assumptions here are certain conditions upon the sum moments of the kernel φ. These applications are true multivariate results which cannot be deduced in any way from unvariate ones. This part of the paper can also be regarded as a contribution to the theory of multivariate spline approximation, dealt with from different sides by [3;5;12;13;15].
Let us finally note that this paper is concerned with direct (Jackson-type) approximation theorems; inverse (Bemstein-type) theorems are studied in [14].
is compared with and deduced from the approximation behaviour of the associated singular convolution integral of Fejér’s type. The matter is applied to three concrete kernels.
The core of this paper is Section 5, devoted to the applications of the general theorems of [6] to box splines, especially to linear combinations of translates of box splines. Basic assumptions here are certain conditions upon the sum moments of the kernel φ. These applications are true multivariate results which cannot be deduced in any way from unvariate ones. This part of the paper can also be regarded as a contribution to the theory of multivariate spline approximation, dealt with from different sides by [3;5;12;13;15].
Let us finally note that this paper is concerned with direct (Jackson-type) approximation theorems; inverse (Bemstein-type) theorems are studied in [14].
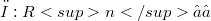 , and a continuous function f the multivariate sampling series is defined by (1.1) (Error rendering LaTeX formula) In [6] the authors presented some qualitative and quantitative theorems on the approximation of
, and a continuous function f the multivariate sampling series is defined by (1.1) (Error rendering LaTeX formula) In [6] the authors presented some qualitative and quantitative theorems on the approximation of 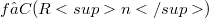 by
by 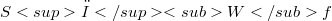 , as well as a few first applications. Some theorems in this respect to be needed below are assertion (5.2) as well as Theorem 5.1 of Section 5. In the more theoretical part of this paper two further quantitative theorems are given. The first deals with the case of product kernels, namely Theorem 3.1, where univariate theory is used to yield convergence theorems with rates in an iterative way, together with an application. The second theorem, Theorem 4.1, is concerned with bandlimited kernels, in which case the convergence with rates of
, as well as a few first applications. Some theorems in this respect to be needed below are assertion (5.2) as well as Theorem 5.1 of Section 5. In the more theoretical part of this paper two further quantitative theorems are given. The first deals with the case of product kernels, namely Theorem 3.1, where univariate theory is used to yield convergence theorems with rates in an iterative way, together with an application. The second theorem, Theorem 4.1, is concerned with bandlimited kernels, in which case the convergence with rates of 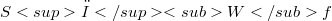 is compared with and deduced from the approximation behaviour of the associated singular convolution integral of Fejér’s type. The matter is applied to three concrete kernels.
The core of this paper is Section 5, devoted to the applications of the general theorems of [6] to box splines, especially to linear combinations of translates of box splines. Basic assumptions here are certain conditions upon the sum moments of the kernel φ. These applications are true multivariate results which cannot be deduced in any way from unvariate ones. This part of the paper can also be regarded as a contribution to the theory of multivariate spline approximation, dealt with from different sides by [3;5;12;13;15].
Let us finally note that this paper is concerned with direct (Jackson-type) approximation theorems; inverse (Bemstein-type) theorems are studied in [14].
is compared with and deduced from the approximation behaviour of the associated singular convolution integral of Fejér’s type. The matter is applied to three concrete kernels.
The core of this paper is Section 5, devoted to the applications of the general theorems of [6] to box splines, especially to linear combinations of translates of box splines. Basic assumptions here are certain conditions upon the sum moments of the kernel φ. These applications are true multivariate results which cannot be deduced in any way from unvariate ones. This part of the paper can also be regarded as a contribution to the theory of multivariate spline approximation, dealt with from different sides by [3;5;12;13;15].
Let us finally note that this paper is concerned with direct (Jackson-type) approximation theorems; inverse (Bemstein-type) theorems are studied in [14].DOI Code:
10.1285/i15900932v10supn1p173
Full Text: PDF


