The exixtence of generalized solutions for a class of linear and nonlinear equations of mixed type
Abstract
In this paper we deal with the question of existence and uniqueness of the generalized solutions for a class of linear and nonlinear equations of the mixed type. In particular we consider 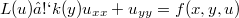 in a simply connected region G , where
in a simply connected region G , where 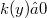 for
for 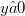 and
and 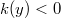 for
for 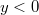 . G is bounded by the curves Γ0,Γ1,Γ2.Γ0
. G is bounded by the curves Γ0,Γ1,Γ2.Γ0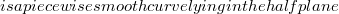 y > 0
y > 0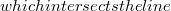 y= 0
y= 0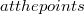 P(- 1,0)
P(- 1,0) Q(0,0)
Q(0,0)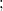 Γ1
Γ1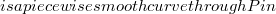 y < (Error rendering LaTeX formula)Γ2(Error rendering LaTeX formula)Γ1$ either lies in the characteristic triangle formed by the characteristics through P and Q (Frankl Problem) or coincides with the characteristics through P (Tricomi Problem). We seek sufficient conditions for the existence and uniqueness of generalized solutions of the boundary problem (Error rendering LaTeX formula)
y < (Error rendering LaTeX formula)Γ2(Error rendering LaTeX formula)Γ1$ either lies in the characteristic triangle formed by the characteristics through P and Q (Frankl Problem) or coincides with the characteristics through P (Tricomi Problem). We seek sufficient conditions for the existence and uniqueness of generalized solutions of the boundary problem (Error rendering LaTeX formula)
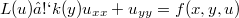 in a simply connected region G , where
in a simply connected region G , where 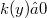 for
for 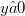 and
and 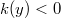 for
for 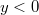 . G is bounded by the curves Γ0,Γ1,Γ2.Γ0
. G is bounded by the curves Γ0,Γ1,Γ2.Γ0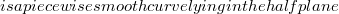 y > 0
y > 0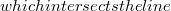 y= 0
y= 0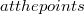 P(- 1,0)
P(- 1,0) Q(0,0)
Q(0,0) Γ1
Γ1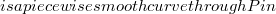 y < (Error rendering LaTeX formula)Γ2(Error rendering LaTeX formula)Γ1$ either lies in the characteristic triangle formed by the characteristics through P and Q (Frankl Problem) or coincides with the characteristics through P (Tricomi Problem). We seek sufficient conditions for the existence and uniqueness of generalized solutions of the boundary problem (Error rendering LaTeX formula)
y < (Error rendering LaTeX formula)Γ2(Error rendering LaTeX formula)Γ1$ either lies in the characteristic triangle formed by the characteristics through P and Q (Frankl Problem) or coincides with the characteristics through P (Tricomi Problem). We seek sufficient conditions for the existence and uniqueness of generalized solutions of the boundary problem (Error rendering LaTeX formula)DOI Code:
10.1285/i15900932v10supn1p47
Keywords:
Linear; Nonlinear; Tricomi-Frankl problem
Classification:
35D05; 35M05
Full Text: PDF


