Newton\'s observations about the field of a uniform thin spherical shell
Abstract
Newton observed that with his law of gravitation the field outside a thin uniform spherical surface is the same as that of a particle at the center, having the same mass as the sphere.He also showed that the field is 0 inside a sphere. We find below all laws of central force having one or the other of these properties. We also formulate the analogous question in two and four (rather than just three) dimensions.We present the findings in a table where, for example, the entry 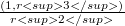 in the place labelled «outside, 3» says that the fields that satisfy the condition outside every sphere in
in the place labelled «outside, 3» says that the fields that satisfy the condition outside every sphere in 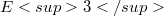 are governed by laws which have any linear combination of 1 and
are governed by laws which have any linear combination of 1 and 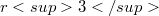 in the numerator, and
in the numerator, and 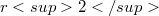 in the denominator.$$ \begin{array}{ccc} \textrm{Dimension} & \textrm{Outside} & \textrm{Inside}\\
2 & \frac{(1,r2)}{r} & \frac{(1,\log r)}{r} \\[5pt]
3 & \frac{(1,r3)}{r2} & \frac{(1,r2)}{r2} \\[5pt]
4 & \frac{(1,r2)}{r3} & \frac{(1,r)}{r3} \end{array}$$.
in the denominator.$$ \begin{array}{ccc} \textrm{Dimension} & \textrm{Outside} & \textrm{Inside}\\
2 & \frac{(1,r2)}{r} & \frac{(1,\log r)}{r} \\[5pt]
3 & \frac{(1,r3)}{r2} & \frac{(1,r2)}{r2} \\[5pt]
4 & \frac{(1,r2)}{r3} & \frac{(1,r)}{r3} \end{array}$$.
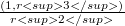 in the place labelled «outside, 3» says that the fields that satisfy the condition outside every sphere in
in the place labelled «outside, 3» says that the fields that satisfy the condition outside every sphere in 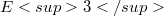 are governed by laws which have any linear combination of 1 and
are governed by laws which have any linear combination of 1 and 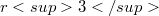 in the numerator, and
in the numerator, and 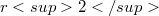 in the denominator.$$ \begin{array}{ccc} \textrm{Dimension} & \textrm{Outside} & \textrm{Inside}\\
2 & \frac{(1,r2)}{r} & \frac{(1,\log r)}{r} \\[5pt]
3 & \frac{(1,r3)}{r2} & \frac{(1,r2)}{r2} \\[5pt]
4 & \frac{(1,r2)}{r3} & \frac{(1,r)}{r3} \end{array}$$.
in the denominator.$$ \begin{array}{ccc} \textrm{Dimension} & \textrm{Outside} & \textrm{Inside}\\
2 & \frac{(1,r2)}{r} & \frac{(1,\log r)}{r} \\[5pt]
3 & \frac{(1,r3)}{r2} & \frac{(1,r2)}{r2} \\[5pt]
4 & \frac{(1,r2)}{r3} & \frac{(1,r)}{r3} \end{array}$$.DOI Code:
10.1285/i15900932v10supn1p39
Full Text: PDF


