Characterizations of almost shrinking bases
Abstract
The material of this paper depends upon the theory of locally convex spaces, sequence spaces and Schauder bases in topological vector spaces and as such we refer to [2] (cf. also [9]), [6] and [7] respectively for several unexpalined definitions, results and terms prevalent in the sequel.However, we do recall a few definitions and terms relevant to the present paper. So, we write thorughout 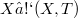 for an arbitrary Hausdorff locally convex space (l.c.s.) with
for an arbitrary Hausdorff locally convex space (l.c.s.) with 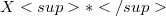 denoting the topological dual of X and
denoting the topological dual of X and 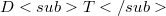 representing the saturated collection of all T-continuous seminorms generating the locally convex (l.c) topology T on X.Also we write the pair of sequences
representing the saturated collection of all T-continuous seminorms generating the locally convex (l.c) topology T on X.Also we write the pair of sequences 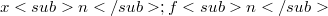 for an arbitrary Schauder basis (S.b.) for X where
for an arbitrary Schauder basis (S.b.) for X where 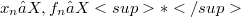 and
and 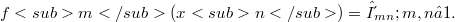 An S.b.
An S.b. 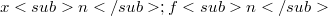 for
for 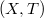 is called shrinking if
is called shrinking if 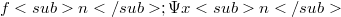 is an S.b. for the strong dual
is an S.b. for the strong dual 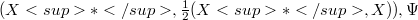 being the usual canonical embedding from X into(Error rendering LaTeX formula)
being the usual canonical embedding from X into(Error rendering LaTeX formula)
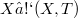 for an arbitrary Hausdorff locally convex space (l.c.s.) with
for an arbitrary Hausdorff locally convex space (l.c.s.) with 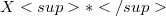 denoting the topological dual of X and
denoting the topological dual of X and 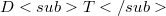 representing the saturated collection of all T-continuous seminorms generating the locally convex (l.c) topology T on X.Also we write the pair of sequences
representing the saturated collection of all T-continuous seminorms generating the locally convex (l.c) topology T on X.Also we write the pair of sequences 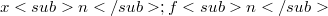 for an arbitrary Schauder basis (S.b.) for X where
for an arbitrary Schauder basis (S.b.) for X where 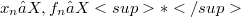 and
and 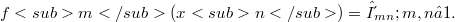 An S.b.
An S.b. 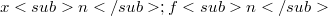 for
for 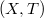 is called shrinking if
is called shrinking if 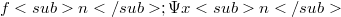 is an S.b. for the strong dual
is an S.b. for the strong dual 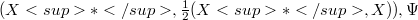 being the usual canonical embedding from X into(Error rendering LaTeX formula)
being the usual canonical embedding from X into(Error rendering LaTeX formula)DOI Code:
10.1285/i15900932v10n1p67
Full Text: PDF


