On types of polynomials and holomorphic functions on Banach spaces
Abstract
In 1966 L. Nachbin introduced the notion of a holomorphy type to consider certain types of polynomials (f.i. compact, nuclear, absolutely summing) in a uniform way [7,8].Holomorphy types with special properties were studied by S. Dineen in 1971 (cf. [4]).Using the well developped theory of linear operator ideals ([9]) various methods of the construction of holomorphy types were presented in [1]. These methods work also in the case of p-normed and quasinormed ideals. After introducing the basic notions the factorization method will be studied here in more details.The main result will be the Theorem 5.1.Of special interest are multilinear operators of type 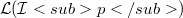 where
where 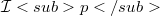 denotes the usual Schatten class of linear operators in Hilbert spaces.These multilinear operators can be characterized by the summablity of their eigenvalues or some other sort of associated sequences of reals (Proposition 4.1).The results will be applied to multilinear operators defined by kernels or convolutions and to holomorphic functions of ideal type.
denotes the usual Schatten class of linear operators in Hilbert spaces.These multilinear operators can be characterized by the summablity of their eigenvalues or some other sort of associated sequences of reals (Proposition 4.1).The results will be applied to multilinear operators defined by kernels or convolutions and to holomorphic functions of ideal type.
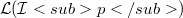 where
where 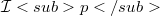 denotes the usual Schatten class of linear operators in Hilbert spaces.These multilinear operators can be characterized by the summablity of their eigenvalues or some other sort of associated sequences of reals (Proposition 4.1).The results will be applied to multilinear operators defined by kernels or convolutions and to holomorphic functions of ideal type.
denotes the usual Schatten class of linear operators in Hilbert spaces.These multilinear operators can be characterized by the summablity of their eigenvalues or some other sort of associated sequences of reals (Proposition 4.1).The results will be applied to multilinear operators defined by kernels or convolutions and to holomorphic functions of ideal type.DOI Code:
10.1285/i15900932v10n1p47
Full Text: PDF


