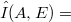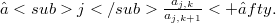On asymptotically normable Fréchet spaces
Abstract
Let E be a Fréchet space, 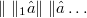 a fundamental system of seminorms on E and U,
a fundamental system of seminorms on E and U, 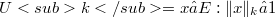 for every k. E is called asymptotically normable, if there is a
for every k. E is called asymptotically normable, if there is a 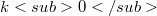 , such that for every
, such that for every 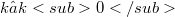 , there is a p so that the seminorms
, there is a p so that the seminorms 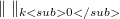 and
and 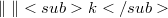 define equivalent topologies on
define equivalent topologies on 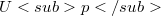 . It is easy to see that in this case
. It is easy to see that in this case 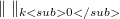 , is in fact a norm. This class of spaces appears in investigations about the structure of Fréchet spaces and about the behaviour of their operators as a natural counterpart of the class of quasi-normable spaces introduced by Grothendieck [4].While the quasi-normable Fréchet spaces E are those which admit an
, is in fact a norm. This class of spaces appears in investigations about the structure of Fréchet spaces and about the behaviour of their operators as a natural counterpart of the class of quasi-normable spaces introduced by Grothendieck [4].While the quasi-normable Fréchet spaces E are those which admit an  -type condition (see[7]) and for which there exists a nontrivial Fréchet space F with
-type condition (see[7]) and for which there exists a nontrivial Fréchet space F with 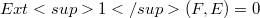 (see [8], [9], [13], [14]), the asymptotically normable Fréchet spaces E are those which admit a DN-type condition (see [13] and below) and for which there exists a nontrivial Fréchet space F with
(see [8], [9], [13], [14]), the asymptotically normable Fréchet spaces E are those which admit a DN-type condition (see [13] and below) and for which there exists a nontrivial Fréchet space F with 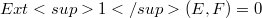 . Nontrivial here could mean: an infinite dimensional nuclear Köthe space. In [7] it is shown that the quasi-normable spaces are the quotient spaces of standard spaces of the form
. Nontrivial here could mean: an infinite dimensional nuclear Köthe space. In [7] it is shown that the quasi-normable spaces are the quotient spaces of standard spaces of the form 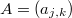 a matrix with
a matrix with 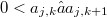 for all k and
for all k and 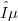 -tensor products and subspaces.The main tool for that is Theorem 3.3. For Schwartz spaces asymptotic normability coincides with countable normability in the sense of Gelfand-Shilov. We show by an example that this even for Montel spaces is not the case.
-tensor products and subspaces.The main tool for that is Theorem 3.3. For Schwartz spaces asymptotic normability coincides with countable normability in the sense of Gelfand-Shilov. We show by an example that this even for Montel spaces is not the case.
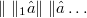 a fundamental system of seminorms on E and U,
a fundamental system of seminorms on E and U, 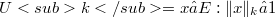 for every k. E is called asymptotically normable, if there is a
for every k. E is called asymptotically normable, if there is a 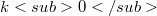 , such that for every
, such that for every 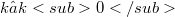 , there is a p so that the seminorms
, there is a p so that the seminorms 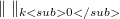 and
and 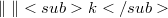 define equivalent topologies on
define equivalent topologies on 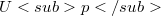 . It is easy to see that in this case
. It is easy to see that in this case 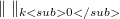 , is in fact a norm. This class of spaces appears in investigations about the structure of Fréchet spaces and about the behaviour of their operators as a natural counterpart of the class of quasi-normable spaces introduced by Grothendieck [4].While the quasi-normable Fréchet spaces E are those which admit an
, is in fact a norm. This class of spaces appears in investigations about the structure of Fréchet spaces and about the behaviour of their operators as a natural counterpart of the class of quasi-normable spaces introduced by Grothendieck [4].While the quasi-normable Fréchet spaces E are those which admit an  -type condition (see[7]) and for which there exists a nontrivial Fréchet space F with
-type condition (see[7]) and for which there exists a nontrivial Fréchet space F with 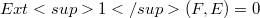 (see [8], [9], [13], [14]), the asymptotically normable Fréchet spaces E are those which admit a DN-type condition (see [13] and below) and for which there exists a nontrivial Fréchet space F with
(see [8], [9], [13], [14]), the asymptotically normable Fréchet spaces E are those which admit a DN-type condition (see [13] and below) and for which there exists a nontrivial Fréchet space F with 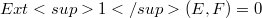 . Nontrivial here could mean: an infinite dimensional nuclear Köthe space. In [7] it is shown that the quasi-normable spaces are the quotient spaces of standard spaces of the form
. Nontrivial here could mean: an infinite dimensional nuclear Köthe space. In [7] it is shown that the quasi-normable spaces are the quotient spaces of standard spaces of the form where E is a Banach space and
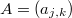 a matrix with
a matrix with 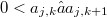 for all k and
for all k and We show that the asymptotically normable spaces are the subspaces of these standard spaces. They are the smallest class of Fréchet spaces which contains the nuclear Köthe spaces with continuous norm, the Banach spaces and is closed under
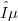 -tensor products and subspaces.The main tool for that is Theorem 3.3. For Schwartz spaces asymptotic normability coincides with countable normability in the sense of Gelfand-Shilov. We show by an example that this even for Montel spaces is not the case.
-tensor products and subspaces.The main tool for that is Theorem 3.3. For Schwartz spaces asymptotic normability coincides with countable normability in the sense of Gelfand-Shilov. We show by an example that this even for Montel spaces is not the case.DOI Code:
10.1285/i15900932v11p289
Full Text: PDF