Local spaces of distributions
Abstract
A space of distributions E is local if, roughly, a distribution T belongs to E whenever T belongs to E in the neighborhood of every point. A space E, in whose definition growth conditions enter, is not local but one can associate with E a local space 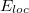 . This is classical for the spaces
. This is classical for the spaces 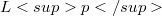 [6], and was done for the Sobolev spaces
[6], and was done for the Sobolev spaces 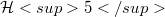 by Laurent Schwartz in his 1956 Bogotà lectures [8], where he presented an expository account of B. Malgrange's doctoral dissertation. In the present paper I establish some simple properties of the space
by Laurent Schwartz in his 1956 Bogotà lectures [8], where he presented an expository account of B. Malgrange's doctoral dissertation. In the present paper I establish some simple properties of the space 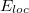 attached to a space of distributions E. To a distribution space E we can also attach the space E, consisting of those elements of E which have compact support. At the end of the paper I make some remarks concerning the duality between local spaces and spaces of distributions with compact support.
attached to a space of distributions E. To a distribution space E we can also attach the space E, consisting of those elements of E which have compact support. At the end of the paper I make some remarks concerning the duality between local spaces and spaces of distributions with compact support.
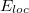 . This is classical for the spaces
. This is classical for the spaces 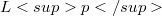 [6], and was done for the Sobolev spaces
[6], and was done for the Sobolev spaces 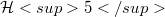 by Laurent Schwartz in his 1956 Bogotà lectures [8], where he presented an expository account of B. Malgrange's doctoral dissertation. In the present paper I establish some simple properties of the space
by Laurent Schwartz in his 1956 Bogotà lectures [8], where he presented an expository account of B. Malgrange's doctoral dissertation. In the present paper I establish some simple properties of the space 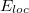 attached to a space of distributions E. To a distribution space E we can also attach the space E, consisting of those elements of E which have compact support. At the end of the paper I make some remarks concerning the duality between local spaces and spaces of distributions with compact support.
attached to a space of distributions E. To a distribution space E we can also attach the space E, consisting of those elements of E which have compact support. At the end of the paper I make some remarks concerning the duality between local spaces and spaces of distributions with compact support.DOI Code:
10.1285/i15900932v11p215
Full Text: PDF


