On the convex compactness property for the strong operator topology
Abstract
In the strong operator topology, the space 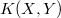 of compact operators between two Banach spaces X, Y is not complete, not even sequentially complete. It is, however, Mackey complete, i.e., every bounded closed absolutely convex subset is a Banach disk (cf. [4]). In this paper we show that
of compact operators between two Banach spaces X, Y is not complete, not even sequentially complete. It is, however, Mackey complete, i.e., every bounded closed absolutely convex subset is a Banach disk (cf. [4]). In this paper we show that 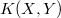 , with the strong operator topology, has a stronger completeness property, namely the convex compactness property (see the definition below).This property is also true for the space of weakly compact operators ([9]).These considerations concerning the convex compactness property of
, with the strong operator topology, has a stronger completeness property, namely the convex compactness property (see the definition below).This property is also true for the space of weakly compact operators ([9]).These considerations concerning the convex compactness property of 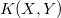 and of other subspaces of
and of other subspaces of 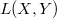 (the space of all continuous linear operators) in the strong operator topology were motivated by the paper of Weis [ 11].They originated from the context of the perturbation theory of
(the space of all continuous linear operators) in the strong operator topology were motivated by the paper of Weis [ 11].They originated from the context of the perturbation theory of 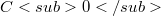 -semigroups, in particular from the application to the neutron transport equation. We refer to [11] as well as to the references quoted there for motivation.
-semigroups, in particular from the application to the neutron transport equation. We refer to [11] as well as to the references quoted there for motivation.
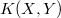 of compact operators between two Banach spaces X, Y is not complete, not even sequentially complete. It is, however, Mackey complete, i.e., every bounded closed absolutely convex subset is a Banach disk (cf. [4]). In this paper we show that
of compact operators between two Banach spaces X, Y is not complete, not even sequentially complete. It is, however, Mackey complete, i.e., every bounded closed absolutely convex subset is a Banach disk (cf. [4]). In this paper we show that 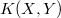 , with the strong operator topology, has a stronger completeness property, namely the convex compactness property (see the definition below).This property is also true for the space of weakly compact operators ([9]).These considerations concerning the convex compactness property of
, with the strong operator topology, has a stronger completeness property, namely the convex compactness property (see the definition below).This property is also true for the space of weakly compact operators ([9]).These considerations concerning the convex compactness property of 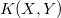 and of other subspaces of
and of other subspaces of 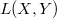 (the space of all continuous linear operators) in the strong operator topology were motivated by the paper of Weis [ 11].They originated from the context of the perturbation theory of
(the space of all continuous linear operators) in the strong operator topology were motivated by the paper of Weis [ 11].They originated from the context of the perturbation theory of  -semigroups, in particular from the application to the neutron transport equation. We refer to [11] as well as to the references quoted there for motivation.
-semigroups, in particular from the application to the neutron transport equation. We refer to [11] as well as to the references quoted there for motivation.DOI Code:
10.1285/i15900932v12p259
Full Text: PDF


