On an abstract form of Weil\'s integrality theorem
Abstract
The purpose of the following discussion is to obtain the classical theorem in the title of this paper as an application of our previous considerations in [29: (i), (ii), (iv), (v)] (an early announcement, under the same title, has been given in [29: (iii)] as well).These, including of course the present study, concern in effect an abstract (axiomatic) approach to the standard differential geometry of 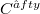 -manifolds and/or of comple(analytic) ones without employing differential calculus at all. So here again one realizes, and essentially in a strengthened way, that «certain [fundamental] quantities which a priori depend on the local diffeerential geometry are actually global topological invariants» (see e.g. [8: Introduction]). Indeed, our treatment is quite topological-algebraic in nature, to the extent that this is accomplished via sheaf theory and, in particular, through sheaf cohomology. Thus, our study might also be viewed as algebraically (viz. operator-theoretically ) oriented. Yet, to make the exposition more comprehensible, we do develop, more or less, the necessary framework for the treatment of the theorem in question, material which, otherwise, is fully discussed in [31]. On the other hand, the connection of the classical Weil's theorem [45] with the theory of geometric quantization is standard (see e.g. [19]). So as a consequence of our study, we also exhibit, in brief (in the final section 9), the result of a similar application of our formulation of the latter theorem (see Theorem 7.1 in the sequel), in conjunction with an interpretation of elementery (free) particles through (sections of) vector sheaves; the latter point of view has been essentially advocated by S.A. Selesnick (cf., for instance, [38]). Finally, we also give in section 8 an outline of particular concrete cases, apart of course from that of the classical differential geometry (real and/or complex), where the present point of view can (in part, see e.g. (8.4) below) be applied. In this respect, it is probably worth noting too that these specific applications come from abstract (commutative)harmonic analysis (cf., for instance, [35], [36] as well as [41],[42]).
-manifolds and/or of comple(analytic) ones without employing differential calculus at all. So here again one realizes, and essentially in a strengthened way, that «certain [fundamental] quantities which a priori depend on the local diffeerential geometry are actually global topological invariants» (see e.g. [8: Introduction]). Indeed, our treatment is quite topological-algebraic in nature, to the extent that this is accomplished via sheaf theory and, in particular, through sheaf cohomology. Thus, our study might also be viewed as algebraically (viz. operator-theoretically ) oriented. Yet, to make the exposition more comprehensible, we do develop, more or less, the necessary framework for the treatment of the theorem in question, material which, otherwise, is fully discussed in [31]. On the other hand, the connection of the classical Weil's theorem [45] with the theory of geometric quantization is standard (see e.g. [19]). So as a consequence of our study, we also exhibit, in brief (in the final section 9), the result of a similar application of our formulation of the latter theorem (see Theorem 7.1 in the sequel), in conjunction with an interpretation of elementery (free) particles through (sections of) vector sheaves; the latter point of view has been essentially advocated by S.A. Selesnick (cf., for instance, [38]). Finally, we also give in section 8 an outline of particular concrete cases, apart of course from that of the classical differential geometry (real and/or complex), where the present point of view can (in part, see e.g. (8.4) below) be applied. In this respect, it is probably worth noting too that these specific applications come from abstract (commutative)harmonic analysis (cf., for instance, [35], [36] as well as [41],[42]).
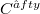 -manifolds and/or of comple(analytic) ones without employing differential calculus at all. So here again one realizes, and essentially in a strengthened way, that «certain [fundamental] quantities which a priori depend on the local diffeerential geometry are actually global topological invariants» (see e.g. [8: Introduction]). Indeed, our treatment is quite topological-algebraic in nature, to the extent that this is accomplished via sheaf theory and, in particular, through sheaf cohomology. Thus, our study might also be viewed as algebraically (viz. operator-theoretically ) oriented. Yet, to make the exposition more comprehensible, we do develop, more or less, the necessary framework for the treatment of the theorem in question, material which, otherwise, is fully discussed in [31]. On the other hand, the connection of the classical Weil's theorem [45] with the theory of geometric quantization is standard (see e.g. [19]). So as a consequence of our study, we also exhibit, in brief (in the final section 9), the result of a similar application of our formulation of the latter theorem (see Theorem 7.1 in the sequel), in conjunction with an interpretation of elementery (free) particles through (sections of) vector sheaves; the latter point of view has been essentially advocated by S.A. Selesnick (cf., for instance, [38]). Finally, we also give in section 8 an outline of particular concrete cases, apart of course from that of the classical differential geometry (real and/or complex), where the present point of view can (in part, see e.g. (8.4) below) be applied. In this respect, it is probably worth noting too that these specific applications come from abstract (commutative)harmonic analysis (cf., for instance, [35], [36] as well as [41],[42]).
-manifolds and/or of comple(analytic) ones without employing differential calculus at all. So here again one realizes, and essentially in a strengthened way, that «certain [fundamental] quantities which a priori depend on the local diffeerential geometry are actually global topological invariants» (see e.g. [8: Introduction]). Indeed, our treatment is quite topological-algebraic in nature, to the extent that this is accomplished via sheaf theory and, in particular, through sheaf cohomology. Thus, our study might also be viewed as algebraically (viz. operator-theoretically ) oriented. Yet, to make the exposition more comprehensible, we do develop, more or less, the necessary framework for the treatment of the theorem in question, material which, otherwise, is fully discussed in [31]. On the other hand, the connection of the classical Weil's theorem [45] with the theory of geometric quantization is standard (see e.g. [19]). So as a consequence of our study, we also exhibit, in brief (in the final section 9), the result of a similar application of our formulation of the latter theorem (see Theorem 7.1 in the sequel), in conjunction with an interpretation of elementery (free) particles through (sections of) vector sheaves; the latter point of view has been essentially advocated by S.A. Selesnick (cf., for instance, [38]). Finally, we also give in section 8 an outline of particular concrete cases, apart of course from that of the classical differential geometry (real and/or complex), where the present point of view can (in part, see e.g. (8.4) below) be applied. In this respect, it is probably worth noting too that these specific applications come from abstract (commutative)harmonic analysis (cf., for instance, [35], [36] as well as [41],[42]).DOI Code:
10.1285/i15900932v12p167
Full Text: PDF


