Aspects of the uniform λ-property
Abstract
If Z is a uniformly convex normed space, the quotient space 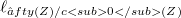 , which is not strictly convexifiable, is shown to have the unifonn λ -property and its
, which is not strictly convexifiable, is shown to have the unifonn λ -property and its 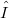 -function is calculated. An example is given of a Banach space X with a closed linear subspace Y such that Y and
-function is calculated. An example is given of a Banach space X with a closed linear subspace Y such that Y and 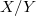 and strictly convex, yet X fails to have the λ- property. Convex sequences which generate
and strictly convex, yet X fails to have the λ- property. Convex sequences which generate 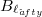 are characterized.
are characterized.
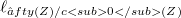 , which is not strictly convexifiable, is shown to have the unifonn λ -property and its
, which is not strictly convexifiable, is shown to have the unifonn λ -property and its 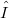 -function is calculated. An example is given of a Banach space X with a closed linear subspace Y such that Y and
-function is calculated. An example is given of a Banach space X with a closed linear subspace Y such that Y and 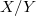 and strictly convex, yet X fails to have the λ- property. Convex sequences which generate
and strictly convex, yet X fails to have the λ- property. Convex sequences which generate 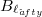 are characterized.
are characterized.DOI Code:
10.1285/i15900932v12p157
Keywords:
Extreme point; Strict convexity; λ-property; Uniform convexity
Full Text: PDF


