On some continued fraction expansions for the ratios of the function
Abstract
In his lost notebook, Ramanujan has defined the function 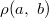 by \begin{equation*} \rho(a ,~b) := \left(1 +\frac{1}{b}\right)\sum_{n=0}^{\infty} \frac{(-1)^{n}q^{n(n+1)/2} {a}^{n}{b}^{-n}}{(-aq)_{n}}, \end{equation*} where
by \begin{equation*} \rho(a ,~b) := \left(1 +\frac{1}{b}\right)\sum_{n=0}^{\infty} \frac{(-1)^{n}q^{n(n+1)/2} {a}^{n}{b}^{-n}}{(-aq)_{n}}, \end{equation*} where 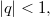 and
and 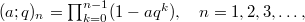 and has given a beautiful reciprocity theorem involving
and has given a beautiful reciprocity theorem involving 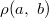 . In this paper we obtain some continued fraction expansions for the ratios of
. In this paper we obtain some continued fraction expansions for the ratios of 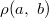 with some of its contiguous functions. We also obtain some interesting special cases of our continued fraction expansions which are analogous to the continued fraction identities stated by Ramanujan. \end
with some of its contiguous functions. We also obtain some interesting special cases of our continued fraction expansions which are analogous to the continued fraction identities stated by Ramanujan. \end
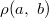 by \begin{equation*} \rho(a ,~b) := \left(1 +\frac{1}{b}\right)\sum_{n=0}^{\infty} \frac{(-1)^{n}q^{n(n+1)/2} {a}^{n}{b}^{-n}}{(-aq)_{n}}, \end{equation*} where
by \begin{equation*} \rho(a ,~b) := \left(1 +\frac{1}{b}\right)\sum_{n=0}^{\infty} \frac{(-1)^{n}q^{n(n+1)/2} {a}^{n}{b}^{-n}}{(-aq)_{n}}, \end{equation*} where 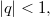 and
and 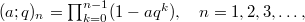 and has given a beautiful reciprocity theorem involving
and has given a beautiful reciprocity theorem involving 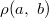 . In this paper we obtain some continued fraction expansions for the ratios of
. In this paper we obtain some continued fraction expansions for the ratios of 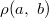 with some of its contiguous functions. We also obtain some interesting special cases of our continued fraction expansions which are analogous to the continued fraction identities stated by Ramanujan. \end
with some of its contiguous functions. We also obtain some interesting special cases of our continued fraction expansions which are analogous to the continued fraction identities stated by Ramanujan. \endDOI Code:
10.1285/i15900932v33n2p35
Keywords:
Basic hypergeometric series; q-continued fractions
Full Text: PDF


