Thenumber of points where a linear mapping from 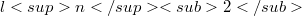 into
into 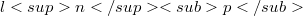 attains its norm
attains its norm
Abstract
Let S be a regular 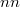 -matrix mapping
-matrix mapping 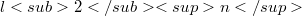 onto
onto 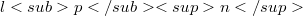 ,
, 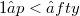 , with norm(Error rendering LaTeX formula). Then we are interested in the set (Error rendering LaTeX formula) i.e. the set of points on the unit sphere where S attains its norm. We prove
, with norm(Error rendering LaTeX formula). Then we are interested in the set (Error rendering LaTeX formula) i.e. the set of points on the unit sphere where S attains its norm. We prove 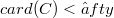 for
for 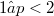 .This follows from properties of the Taylor expansion of
.This follows from properties of the Taylor expansion of 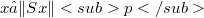 near points in C. The case
near points in C. The case 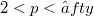 remains open. But we show by an example that for
remains open. But we show by an example that for 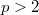 the behaviour of
the behaviour of 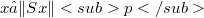 may be completely different as for
may be completely different as for 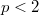 .
.
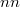 -matrix mapping
-matrix mapping 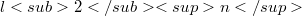 onto
onto 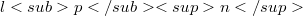 ,
, 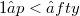 , with norm(Error rendering LaTeX formula). Then we are interested in the set (Error rendering LaTeX formula) i.e. the set of points on the unit sphere where S attains its norm. We prove
, with norm(Error rendering LaTeX formula). Then we are interested in the set (Error rendering LaTeX formula) i.e. the set of points on the unit sphere where S attains its norm. We prove 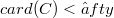 for
for 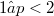 .This follows from properties of the Taylor expansion of
.This follows from properties of the Taylor expansion of 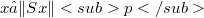 near points in C. The case
near points in C. The case 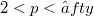 remains open. But we show by an example that for
remains open. But we show by an example that for 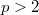 the behaviour of
the behaviour of 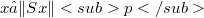 may be completely different as for
may be completely different as for 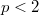 .
.DOI Code:
10.1285/i15900932v12p145
Full Text: PDF


