The contact Whitney sphere

Abstract

In this paper, we introduce the contact Whitney sphere as an imbedding of the 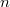--dimensional unit sphere as an integral submanifold of the standard contact structure on 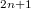. We obtain a general inequality for integral submanifolds in 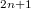, involving both the scalar curvature and the mean curvature, and we use the equality case in order to characterize the contact Whitney sphere. We also study a similar problem foranti-invariant submanifolds of 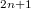, tangent to the structure vector field.