Space curves not contained in low degree surfaces in positive characteristic

E. Ballico

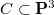Let $C \subset \mathbf{P}^3$ be an integral projective curve not contained in a quadric surface. Set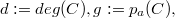 $d:=deg(C),g:=p_a(C),$

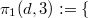
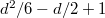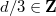
$\pi_1(d,3):= \left\{$ $d^2/6 - d/2 + 1$ if $d/3 \in \mathbf{Z}$
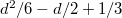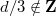
$d^2/6 - d/2 + 1/3$ if $d/3 \notin \mathbf{Z}$ $\right$ .

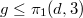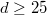Here we prove in arbitrary characteristic that $g \le \pi_1(d,3)$ if $d \ge 25$ .

DOI Code: 10.1285/i15900932v20n2p27

Keywords: Integral projective curve; Singular space curve; Arithmetic genus; Quadric surface; Plane section; Hyperplane section; Hilbert function

Classification: 14H50

Full Text: PDF

Note di Matematica