On a generalization of Posthumus graphs
Abstract
In graph theory one often deals with 1-graphs (i. e.:given two vertices u and v, there is at last one arc that incides from u to v) of order 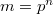 , where
, where  and
and 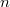 are natural number greater than
are natural number greater than 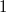 . These are regular graphs of degree
. These are regular graphs of degree  and diameter
and diameter 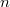 , which have a certain importance in some problems of telecommunication (cf. [2], p.229: EXAMPLE), since vertices and arcs can respectively represent stations and one-way connections of a telecommunication network.
, which have a certain importance in some problems of telecommunication (cf. [2], p.229: EXAMPLE), since vertices and arcs can respectively represent stations and one-way connections of a telecommunication network.
It seems that the first construction of these graphs, with 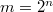 , is due to Ir. K. Posthumus, who stated a very interesting conjecture, concerning some cycles of digits 0 or 1, proved in [1] by N. G. De Bruijn.\\In the study of these graphs the condition
, is due to Ir. K. Posthumus, who stated a very interesting conjecture, concerning some cycles of digits 0 or 1, proved in [1] by N. G. De Bruijn.\\In the study of these graphs the condition 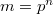 is heavily relied on. In this paper we adapt that construction to the case in which
is heavily relied on. In this paper we adapt that construction to the case in which 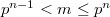 ; so we find again several interesting properties of the previous particular case.\\Among other things, we get regular 1-graphs of degree
; so we find again several interesting properties of the previous particular case.\\Among other things, we get regular 1-graphs of degree  , such that for any two different vertices
, such that for any two different vertices 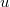 and
and  there exists at least a path from
there exists at least a path from 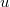 to
to  of length less than, or equal to,
of length less than, or equal to, 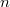 .
.
Full Text: PDF


