Isomorphisms between lattices of nearly normal subgroups
Abstract
A subgroup 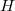 of a group
of a group  is said to be nearly normal in
is said to be nearly normal in  if it has a finite index in its normal closure
if it has a finite index in its normal closure 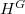 . The set nn(G) of nearly normal subgroups of
. The set nn(G) of nearly normal subgroups of  is a sublattice of the lattice of all subgroups of
is a sublattice of the lattice of all subgroups of  . Isomorphisms between lattices of nearly normal subgroups of
. Isomorphisms between lattices of nearly normal subgroups of 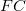 -soluble groups are considered in this paper. In particular, properties of images of normal subgroups under such an isomorphism are investigated. Moreover, it is proved that if
-soluble groups are considered in this paper. In particular, properties of images of normal subgroups under such an isomorphism are investigated. Moreover, it is proved that if  is a supersoluble group and
is a supersoluble group and 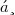 is an
is an 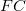 -soluble group such that the lattices nn(G)and nn(Ḡ) are isomorphic, then also Ḡ is supersoluble.
-soluble group such that the lattices nn(G)and nn(Ḡ) are isomorphic, then also Ḡ is supersoluble.
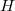 of a group
of a group  is said to be nearly normal in
is said to be nearly normal in  if it has a finite index in its normal closure
if it has a finite index in its normal closure 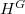 . The set nn(G) of nearly normal subgroups of
. The set nn(G) of nearly normal subgroups of  is a sublattice of the lattice of all subgroups of
is a sublattice of the lattice of all subgroups of  . Isomorphisms between lattices of nearly normal subgroups of
. Isomorphisms between lattices of nearly normal subgroups of 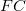 -soluble groups are considered in this paper. In particular, properties of images of normal subgroups under such an isomorphism are investigated. Moreover, it is proved that if
-soluble groups are considered in this paper. In particular, properties of images of normal subgroups under such an isomorphism are investigated. Moreover, it is proved that if  is a supersoluble group and
is a supersoluble group and 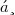 is an
is an 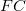 -soluble group such that the lattices nn(G)and nn(Ḡ) are isomorphic, then also Ḡ is supersoluble.
-soluble group such that the lattices nn(G)and nn(Ḡ) are isomorphic, then also Ḡ is supersoluble.DOI Code:
10.1285/i15900932v20n1p43
Keywords:
Nearly normal subgroup; Lattice isomorphism
Classification:
20F24
Full Text: PDF


