More on 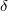 -semiopen sets
-semiopen sets
Abstract
In 1963, Levine [2] introduced the notion of semi-open sets which is weaker than the notion of open sets in topological spaces. Since then several interesting generalized open sets came to existence. In 1968, Velicko [5] introduced 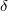 -open sets, which are stronger than open sets, in order to investigate the characterization of H-closed spaces. In 1997, Park et al.[4] have offered a new notion called
-open sets, which are stronger than open sets, in order to investigate the characterization of H-closed spaces. In 1997, Park et al.[4] have offered a new notion called 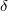 -semiopen sets which are stronger than semi-open sets but weaker than
-semiopen sets which are stronger than semi-open sets but weaker than 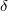 -open sets. They also studied the relationships between these sets and several other types of open sets. It is the aim of this paper to offer some weak separation axioms by utilizing
-open sets. They also studied the relationships between these sets and several other types of open sets. It is the aim of this paper to offer some weak separation axioms by utilizing 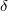 -semiopen sets and the
-semiopen sets and the 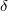 -semi-closure operator.
-semi-closure operator.
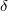 -open sets, which are stronger than open sets, in order to investigate the characterization of H-closed spaces. In 1997, Park et al.[4] have offered a new notion called
-open sets, which are stronger than open sets, in order to investigate the characterization of H-closed spaces. In 1997, Park et al.[4] have offered a new notion called 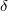 -semiopen sets which are stronger than semi-open sets but weaker than
-semiopen sets which are stronger than semi-open sets but weaker than 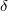 -open sets. They also studied the relationships between these sets and several other types of open sets. It is the aim of this paper to offer some weak separation axioms by utilizing
-open sets. They also studied the relationships between these sets and several other types of open sets. It is the aim of this paper to offer some weak separation axioms by utilizing 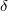 -semiopen sets and the
-semiopen sets and the 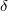 -semi-closure operator.
-semi-closure operator.DOI Code:
10.1285/i15900932v22n2p113
Keywords:
δ-semiopen set; δ-semiD-set; δ-semi$D0$; δ-semi$D1$; δ-semi$D2$; Sober δ-semi$R0$; δ-semi$R0$; δ-semi$R1$
Classification:
54B05; 54C08
Full Text: PDF


