Spreads in 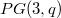 admitting several homology groups of order
admitting several homology groups of order 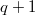
Abstract
The set of translation planes with spreads in 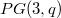 admitting at least three homology groups with distinct axes of order
admitting at least three homology groups with distinct axes of order 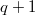 is completely determined. Apart from the Desarguesian and Hall planes of order
is completely determined. Apart from the Desarguesian and Hall planes of order 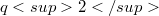 , the only possible plane is the Heimbeck plane of order
, the only possible plane is the Heimbeck plane of order 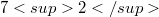 admitting several quaternion homology groups of order 8. A classification is also given of all translation planes with spreads in
admitting several quaternion homology groups of order 8. A classification is also given of all translation planes with spreads in 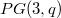 that admit at least three distinct homology groups of order
that admit at least three distinct homology groups of order 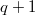 . Recent results conneting translation planes with spreads in
. Recent results conneting translation planes with spreads in 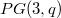 admitting cyclic affine homology groups of order
admitting cyclic affine homology groups of order 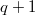 with conical flocks spreads provide the background for applications showing how the associated collineation groups are interrelated.
with conical flocks spreads provide the background for applications showing how the associated collineation groups are interrelated.
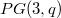 admitting at least three homology groups with distinct axes of order
admitting at least three homology groups with distinct axes of order 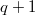 is completely determined. Apart from the Desarguesian and Hall planes of order
is completely determined. Apart from the Desarguesian and Hall planes of order 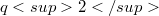 , the only possible plane is the Heimbeck plane of order
, the only possible plane is the Heimbeck plane of order 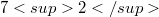 admitting several quaternion homology groups of order 8. A classification is also given of all translation planes with spreads in
admitting several quaternion homology groups of order 8. A classification is also given of all translation planes with spreads in 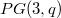 that admit at least three distinct homology groups of order
that admit at least three distinct homology groups of order 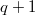 . Recent results conneting translation planes with spreads in
. Recent results conneting translation planes with spreads in 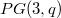 admitting cyclic affine homology groups of order
admitting cyclic affine homology groups of order 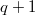 with conical flocks spreads provide the background for applications showing how the associated collineation groups are interrelated.
with conical flocks spreads provide the background for applications showing how the associated collineation groups are interrelated.DOI Code:
10.1285/i15900932v24n2p9
Keywords:
Homology groups; Translation planes; Spreads; Flocks of quadratic cones; Hyperbolic fibrations
Classification:
51E23; 51A40
Full Text: PDF


