Translation planes of order 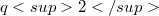 admitting collineation groups of order
admitting collineation groups of order 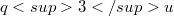 preserving a parabolic unital
preserving a parabolic unital
Abstract
The set of translation planes of order 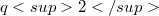 that admit collineation groups of order
that admit collineation groups of order 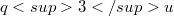 , where u is a prime p-primitive divisor of
, where u is a prime p-primitive divisor of 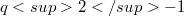 , consists of exactly the Desarguesian plane, assuming that the group does not contain a translation subgroup of order a multiple of
, consists of exactly the Desarguesian plane, assuming that the group does not contain a translation subgroup of order a multiple of 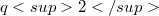 . This applies to show that if the group preserves a parabolic unital then the plane is forced to be Desarguesian.
. This applies to show that if the group preserves a parabolic unital then the plane is forced to be Desarguesian.
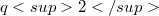 that admit collineation groups of order
that admit collineation groups of order 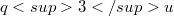 , where u is a prime p-primitive divisor of
, where u is a prime p-primitive divisor of 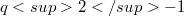 , consists of exactly the Desarguesian plane, assuming that the group does not contain a translation subgroup of order a multiple of
, consists of exactly the Desarguesian plane, assuming that the group does not contain a translation subgroup of order a multiple of 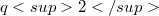 . This applies to show that if the group preserves a parabolic unital then the plane is forced to be Desarguesian.
. This applies to show that if the group preserves a parabolic unital then the plane is forced to be Desarguesian.DOI Code:
10.1285/i15900932v26n2p105
Keywords:
Spread; Translation plane; Parabolic unital; Unital group
Classification:
51E23; 51A40
Full Text: PDF


