Multiplicatively closed bases for 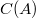
Abstract
A canonical basis for the centralizer 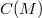 of a
of a 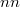 complex matrix M is obtained from the one
complex matrix M is obtained from the one 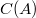 constructed for a Jordan canonical form A of M. These bases are closed under nonzero products and we obtain simple multiplication tables for their products. Two matrices have the same centralizer invariants iff their Jordan canonical forms have the same block structure. For square matrices M and N we prove that
constructed for a Jordan canonical form A of M. These bases are closed under nonzero products and we obtain simple multiplication tables for their products. Two matrices have the same centralizer invariants iff their Jordan canonical forms have the same block structure. For square matrices M and N we prove that 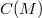 and
and 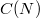 are isomorphic as algebras over C iff they have the same size and the same centralizer invariants. We produce a similar canonical basis for the centralizer algebra of a real matrix over the real numbers which has analogous multiplicative properties in addition to conjugation properties. We also give some additional consequences of these results.
are isomorphic as algebras over C iff they have the same size and the same centralizer invariants. We produce a similar canonical basis for the centralizer algebra of a real matrix over the real numbers which has analogous multiplicative properties in addition to conjugation properties. We also give some additional consequences of these results.
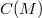 of a
of a 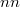 complex matrix M is obtained from the one
complex matrix M is obtained from the one 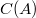 constructed for a Jordan canonical form A of M. These bases are closed under nonzero products and we obtain simple multiplication tables for their products. Two matrices have the same centralizer invariants iff their Jordan canonical forms have the same block structure. For square matrices M and N we prove that
constructed for a Jordan canonical form A of M. These bases are closed under nonzero products and we obtain simple multiplication tables for their products. Two matrices have the same centralizer invariants iff their Jordan canonical forms have the same block structure. For square matrices M and N we prove that 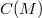 and
and 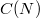 are isomorphic as algebras over C iff they have the same size and the same centralizer invariants. We produce a similar canonical basis for the centralizer algebra of a real matrix over the real numbers which has analogous multiplicative properties in addition to conjugation properties. We also give some additional consequences of these results.
are isomorphic as algebras over C iff they have the same size and the same centralizer invariants. We produce a similar canonical basis for the centralizer algebra of a real matrix over the real numbers which has analogous multiplicative properties in addition to conjugation properties. We also give some additional consequences of these results.DOI Code:
10.1285/i15900932v26n2p81
Keywords:
Centralizer algebra; Matrix; Basis; Center
Classification:
15A21; 15A30
Full Text: PDF


