Girth 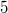 Graphs from Elliptic Semiplanes
Graphs from Elliptic Semiplanes
Abstract
For 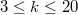 with
with 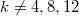 , all the smallestcurrently known
, all the smallestcurrently known 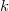 --regular graphs of girth
--regular graphs of girth 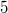 have the sameorders as the girth
have the sameorders as the girth 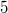 graphs obtained by the followingconstruction: take a (not necessarily Desarguesian) ellipticsemiplane
graphs obtained by the followingconstruction: take a (not necessarily Desarguesian) ellipticsemiplane 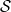 of order
of order 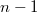 where
where 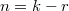 for some
for some 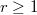 ; the Levi graph
; the Levi graph 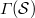 of
of 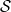 is an
is an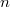 --regular graph of girth
--regular graph of girth 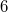 ; parallel classes of
; parallel classes of 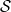 induce co--cliques in
induce co--cliques in 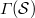 , some of which areeventually deleted; the remaining co--cliques are amalgamated withsuitable
, some of which areeventually deleted; the remaining co--cliques are amalgamated withsuitable  --regular graphs of girth at least
--regular graphs of girth at least 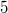 . For
. For 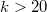 ,this construction yields some new instances underbidding thesmallest orders known so far.
,this construction yields some new instances underbidding thesmallest orders known so far.
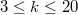 with
with 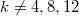 , all the smallestcurrently known
, all the smallestcurrently known 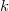 --regular graphs of girth
--regular graphs of girth 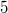 have the sameorders as the girth
have the sameorders as the girth 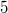 graphs obtained by the followingconstruction: take a (not necessarily Desarguesian) ellipticsemiplane
graphs obtained by the followingconstruction: take a (not necessarily Desarguesian) ellipticsemiplane 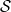 of order
of order 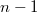 where
where 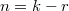 for some
for some 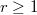 ; the Levi graph
; the Levi graph 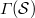 of
of 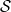 is an
is an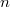 --regular graph of girth
--regular graph of girth 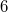 ; parallel classes of
; parallel classes of 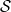 induce co--cliques in
induce co--cliques in 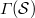 , some of which areeventually deleted; the remaining co--cliques are amalgamated withsuitable
, some of which areeventually deleted; the remaining co--cliques are amalgamated withsuitable  --regular graphs of girth at least
--regular graphs of girth at least 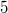 . For
. For 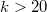 ,this construction yields some new instances underbidding thesmallest orders known so far.
,this construction yields some new instances underbidding thesmallest orders known so far.DOI Code:
10.1285/i15900932v29n1supplp91
Keywords:
(k,5)-cages; girth 5 graphs; elliptic semiplanes; Hughes planes
(k,5)-cages; girth 5 graphs; elliptic semiplanes; Hughes planes
Full Text: PDF


