Generalized 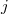 -planes
-planes
Abstract
We construct and study a class of translation planes with kernel 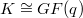 , order
, order 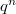 , and
, and 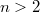 . These planes generalize the
. These planes generalize the 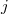 -planes discovered by Johnson, Pomareda and Wilke in [14]. We show these planes are actually
-planes discovered by Johnson, Pomareda and Wilke in [14]. We show these planes are actually 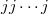 -planes. Hence, most of the results obtained in this article are on
-planes. Hence, most of the results obtained in this article are on 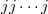 -planes. In fact, our study shows that these planes are either nearfield or new.
-planes. In fact, our study shows that these planes are either nearfield or new.
An infinite class of nearfield 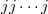 -planes is shown to exist, and a finite set of sporadic non-Andr\'e
-planes is shown to exist, and a finite set of sporadic non-Andr\'e 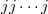 -planes is presented.
-planes is presented.
DOI Code:
10.1285/i15900932v29n2p143
Keywords:
Translation planes, homology groups, nets, j-planes
Translation planes, homology groups, nets, j-planes
Full Text: PDF


