On the extrinsic principal directions of Riemannian submanifolds
Abstract
The Casorati curvature of a submanifold 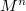 of a Riemannianmanifold
of a Riemannianmanifold 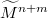 is known to be the normalized square of the lengthof the second fundamental form,
is known to be the normalized square of the lengthof the second fundamental form, 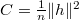 , i.e., inparticular, for hypersurfaces,
, i.e., inparticular, for hypersurfaces, 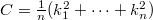 , whereby
, whereby 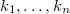 are the principal normalcurvatures of these hypersurfaces. In this paper we in additiondefine the Casorati curvature of a submanifold
are the principal normalcurvatures of these hypersurfaces. In this paper we in additiondefine the Casorati curvature of a submanifold 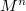 in aRiemannian manifold
in aRiemannian manifold 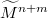 at any point
at any point  of
of 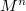 in any tangentdirection
in any tangentdirection 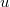 of
of 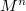 . The principal extrinsic (Casorati)directions of a submanifold at a point are defined as an extensionof the principal directions of a hypersurface
. The principal extrinsic (Casorati)directions of a submanifold at a point are defined as an extensionof the principal directions of a hypersurface 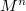 at a point in
at a point in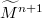 . A geometrical interpretation of the Casorati curvature of
. A geometrical interpretation of the Casorati curvature of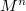 in
in 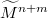 at
at  in the direction
in the direction 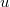 is given. Acharacterization of normally flat submanifolds in Euclidean spacesis given in terms of a relation between the Casorati curvaturesand the normal curvatures of these submanifolds.
is given. Acharacterization of normally flat submanifolds in Euclidean spacesis given in terms of a relation between the Casorati curvaturesand the normal curvatures of these submanifolds.
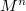 of a Riemannianmanifold
of a Riemannianmanifold 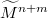 is known to be the normalized square of the lengthof the second fundamental form,
is known to be the normalized square of the lengthof the second fundamental form, 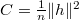 , i.e., inparticular, for hypersurfaces,
, i.e., inparticular, for hypersurfaces, 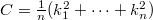 , whereby
, whereby 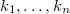 are the principal normalcurvatures of these hypersurfaces. In this paper we in additiondefine the Casorati curvature of a submanifold
are the principal normalcurvatures of these hypersurfaces. In this paper we in additiondefine the Casorati curvature of a submanifold 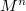 in aRiemannian manifold
in aRiemannian manifold 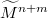 at any point
at any point  of
of 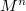 in any tangentdirection
in any tangentdirection 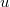 of
of 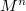 . The principal extrinsic (Casorati)directions of a submanifold at a point are defined as an extensionof the principal directions of a hypersurface
. The principal extrinsic (Casorati)directions of a submanifold at a point are defined as an extensionof the principal directions of a hypersurface 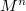 at a point in
at a point in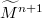 . A geometrical interpretation of the Casorati curvature of
. A geometrical interpretation of the Casorati curvature of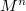 in
in 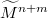 at
at  in the direction
in the direction 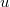 is given. Acharacterization of normally flat submanifolds in Euclidean spacesis given in terms of a relation between the Casorati curvaturesand the normal curvatures of these submanifolds.
is given. Acharacterization of normally flat submanifolds in Euclidean spacesis given in terms of a relation between the Casorati curvaturesand the normal curvatures of these submanifolds.DOI Code:
10.1285/i15900932v29n2p41
Keywords:
Casorati curvature; principal direction; normal curvature; squared length of the second fundamental form
Casorati curvature; principal direction; normal curvature; squared length of the second fundamental form
Full Text: PDF


