On a paper of Dan Barbilian
Abstract
En
We point out that the axiomatic analysis of the statement The segments joining a point with the vertices of an equilateral triangle satisfy the (non-strict) triangle inequalities in Barbilian’s [1] misses the case in which the sum of the angles in a triangle is greater than 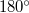 .
.
We situate the statement correctly inside absolute geometry. We also point out that [1] contains the first proof that a Hilbert geometry with symmetric perpendicularity must be hyperbolic geometry, a proof commonly attributed to P. J. Kelly and L. J. Paige [5].
DOI Code:
10.1285/i15900932v29n2p29
Keywords:
Hilbert geometry; the Mòbius-Pompeiu inequality; absolute geometry
Hilbert geometry; the Mòbius-Pompeiu inequality; absolute geometry
Full Text: PDF


