On not open linear continuous operators between Banach spaces
Abstract
Let X and Y be infinite-dimensional Banach spaces. Let 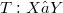 be a linear continuous operator with dense range and
be a linear continuous operator with dense range and 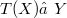 . It is proved that, for each
. It is proved that, for each 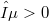 , there exists a quotient map
, there exists a quotient map 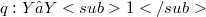 , such that
, such that 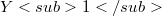 is an infinite-dimensional Banach space with a Schauder basis and
is an infinite-dimensional Banach space with a Schauder basis and 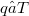 is a nuclear operator of norm
is a nuclear operator of norm 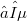 . Thereby, we obtain with respect to the quotient spaces the proper analogue result of Kato concerning the existence of not trivial nuclear restrictions of not open linear continuous operators between Banach spaces.
As a consequence, it is derived a result of Ostrovskii concerning Banach spaces which are completions with respect to total nonnorming subspaces.
. Thereby, we obtain with respect to the quotient spaces the proper analogue result of Kato concerning the existence of not trivial nuclear restrictions of not open linear continuous operators between Banach spaces.
As a consequence, it is derived a result of Ostrovskii concerning Banach spaces which are completions with respect to total nonnorming subspaces.
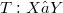 be a linear continuous operator with dense range and
be a linear continuous operator with dense range and 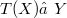 . It is proved that, for each
. It is proved that, for each 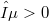 , there exists a quotient map
, there exists a quotient map 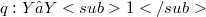 , such that
, such that 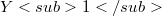 is an infinite-dimensional Banach space with a Schauder basis and
is an infinite-dimensional Banach space with a Schauder basis and 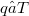 is a nuclear operator of norm
is a nuclear operator of norm 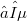 . Thereby, we obtain with respect to the quotient spaces the proper analogue result of Kato concerning the existence of not trivial nuclear restrictions of not open linear continuous operators between Banach spaces.
As a consequence, it is derived a result of Ostrovskii concerning Banach spaces which are completions with respect to total nonnorming subspaces.
. Thereby, we obtain with respect to the quotient spaces the proper analogue result of Kato concerning the existence of not trivial nuclear restrictions of not open linear continuous operators between Banach spaces.
As a consequence, it is derived a result of Ostrovskii concerning Banach spaces which are completions with respect to total nonnorming subspaces.DOI Code:
10.1285/i15900932v25n1p29
Keywords:
Not open linear continuous operators; Nuclear operators; Basic sequence; Biorthogonal system; Quotient spaces
Classification:
46B20; 47A65; 47B10
Full Text: PDF


