The Maximality of the Group of Euclidean Similarities within the Affine Group
Abstract
The purpose of this note is to show by elementary means that over the field of real numbers, or more generally over any Euclidean field K with Archimedean order the group of n-dimensional Euclidean similarities is maximal within the group of all affine mappings having a determinant of the form 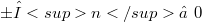 . As a corollary it turns out that the orthogonal group
. As a corollary it turns out that the orthogonal group 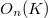 is maximal within the group
is maximal within the group 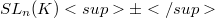 of all matrices of determinant
of all matrices of determinant 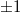 .
.
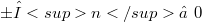 . As a corollary it turns out that the orthogonal group
. As a corollary it turns out that the orthogonal group 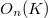 is maximal within the group
is maximal within the group 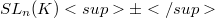 of all matrices of determinant
of all matrices of determinant 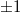 .
.DOI Code:
10.1285/i15900932v19n1p33
Full Text: PDF


